Calculating Yards of Concrete: Explained

Calculating yards of concrete is important in every concrete job. In fact, it is vital to perform precise calculations so that you do not end up ordering much more or less than needed.

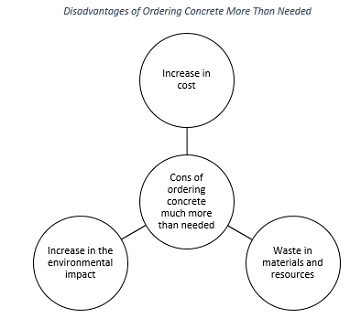
On one hand, ordering much more cubic yards of concrete than needed is basically an undesired increase in costs and waste in materials and resources.

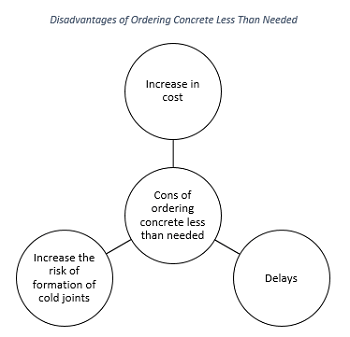
On the other hand, ordering less yards of concrete than needed is also an undesired increase in costs, since it requires reordering a short load, which has a higher unit price. In addition, these delays not only increase the labor costs, but also increase the risk of cold joints.

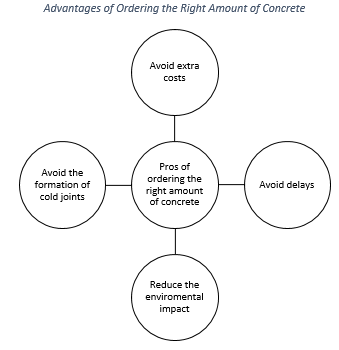
Thereby, precisely calculating yards of concrete can save you money and time, reduce the environmental impact, and avoid problems such as the formation of cold joints.

However, ordering the exact yardage, or calculating bags of concrete based on the exact yardage, is not always the best practice. You should account for material waste and slight measurement or calculation errors. Besides, it is always best to order slightly more than needed instead of ending up short on concrete. Thereby, calculating yards of concrete with the addition of about 5% is beneficial.

How to calculate how many yards of concrete do you need for different applications?

Calculating yards of concrete is in fact very simple. It is basically the process of calculating the volume that needs to be filled with concrete. These calculations often use simple mathematical equations, depending on the shape of the object. For example, slabs, columns, holes, beams, and walls, often have the shape of a rectangle, square, or a circle.

Slabs

Most slabs have a uniform shape, which simplifies calculating their volume. However, non-uniform slabs also exist, and calculating their volume is also usually straight forward.

Uniform slabs

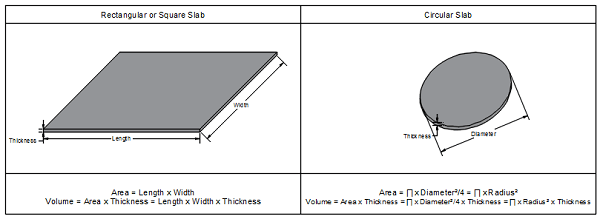
Uniformly shaped slabs mostly include rectangular, square, and circular slabs with constant thickness. For such slabs, calculating yards of concrete is as simple as calculating the area, then multiplying it by the thickness.
For example, you can calculate the area of a rectangular slab by multiplying its length by its width. Hence, its volume will be (length x width x thickness).
For square slabs, you can apply the same equation as that in the rectangular. The only difference is that the sides of a square are equal.
For circular slabs, you can calculate the area by either using (3.1415 x diameter x diameter / 4), or (3.1415 x radius x radius). Hence, the volume will be (3.1415 x diameter x diameter x thickness / 4), or (3.1415 x radius x radius x thickness).

Uniform slab example

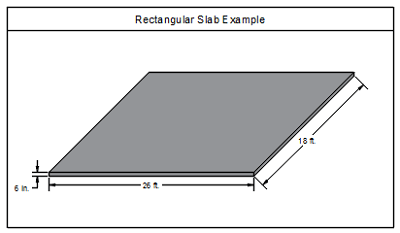
Considering the following example, the rectangular slab is 26 feet long, 18 feet wide, and 6 inches thick. However, for calculating yards of concrete, or cubic yards, we have to convert all the units from feet and inches to yards.
Note, 3 feet equals 1 yard, and each 36 inches equal 1 yard.

Area = length x width = 26ft x 18ft = 468 square feet = 52 square yards.
Volume = area x thickness = 52 square yards x 6/36 = 8.66 cubic yards.

Hence, the calculated yards of concrete for this slab is 8.66 cubic yards. However, taking into account waste, dimension errors (slight thickness variations due to base preparation for example), or slight finishing thickness variations, you can add about 5%. Thus, you can order 9 cubic yards, which is almost 3.85% more than needed.

Non-uniform slabs

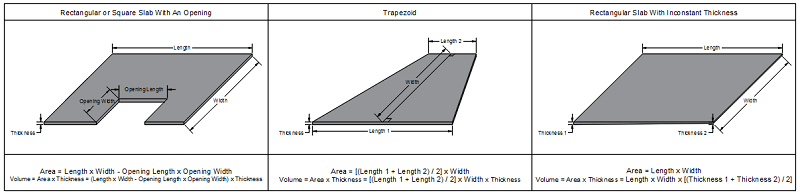
Non-uniformly shaped slabs include irregular shapes, combined regular shapes, or inconstant thickness. However, calculating yards of concrete for these slabs requires dividing the shape into smaller regular parts or calculating the average of some dimensions in order to simplify your calculations.

Non-uniform slab example

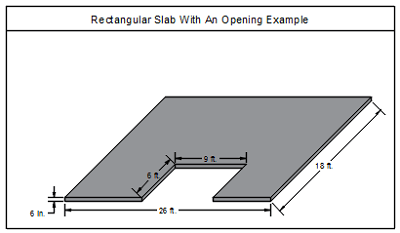
Calculating yards of concrete for the following irregular shape requires first to divide the given shape into regular shapes. Then, the volumes of these regular shapes can be added or subtracted in order to get the required volume.

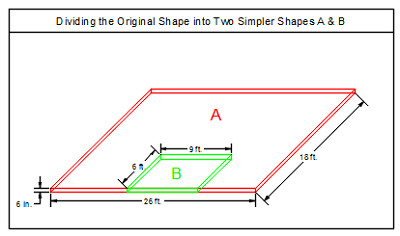
Hence, the following example now represents a slab (A) having a length of 26 feet, width of 18 feet, thickness of 6 inches, with a cut portion (B) having a length of 9 feet, width of 6 feet, and thickness of 6 inches.
The required volume = Volume (A) – Volume (B).
Where the volume of each equals (length x width x thickness), converting the units from feet and inches to yards, where 3 feet equals 1 yard, and each 36 inches equal 1 yard.

Volume (A) = (26/3) x (18/3) x (6/36) = 8.66 cubic yards.
Volume (B) = (9/3) x (6/3) x (6/36) = 1 cubic yard.
Required volume = 8.66 – 1 = 7.66 cubic yards.

Thereby, the calculated yards of concrete is 7.66. However, it is recommended to order slightly more to account for any slight dimension errors, material waste, finishing accuracy, and other factors. Thereby, you can 8 cubic yards, which is about 4.35% more than the calculated value.

Columns and holes

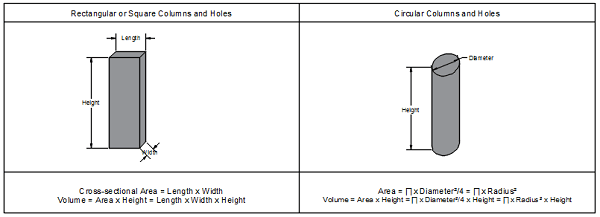
Columns and holes are usually either rectangular, square, or circular. Hence, calculating yards of concrete or volume is relatively simple. You can calculate the volume by multiplying the area by the height.
For example, the area of a rectangular or a square column and holes equals (length x width). Hence, the volume equals (length x width x height).
For circular columns and holes, the area equals (3.1415 x diameter x diameter / 4), or (3.1415 x radius x radius). Thereby, the volume equals (3.1415 x diameter x diameter x height / 4), or (3.1415 x radius x radius x height).

Columns example

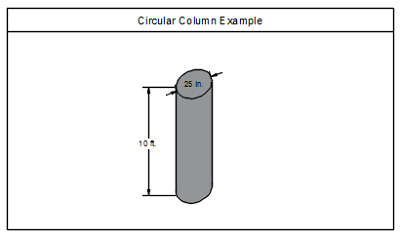
For the given example, the circular column has a diameter of 25 inches and a height if 10 feet. However, for calculating yards of concrete, we should convert the dimensions from inches and feet to yards, where 1 yard converts to 36 inches, or 3 feet.

Area = 3.1415 x 25 x 25 / 4 = 490.86 square inches = 0.378 square yards.
Or, area = 3.1415 x (25/2) x (25/2) = 490.86 square inches = 0.378 square yards.
Volume = area x height = 0.378 x 10/36 = 0.105 cubic yards.

Beams

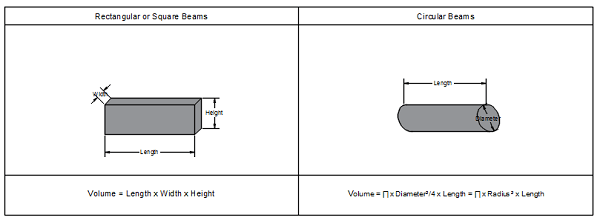
Beams also usually have rectangular, square, or circular shapes. In fact, calculating yards of concrete for beams is very similar to columns or holes; the main difference is that columns are vertical elements, whereas beams are horizontal elements.
For square and rectangular beams, the volume equals (length x width x height or depth).
For circular beams, the volume equals (3.1415 x diameter x diameter x height / 4), or (3.1415 x radius x radius x height).

Beams example

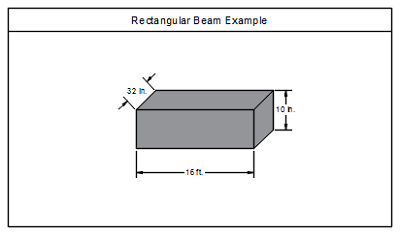
In the following example, the beam has a length of 16 feet, width of 32 inches, and height or depth of 10 inches. Also, similar to previous examples, calculating yards of concrete requires converting units from feet and inches to yards, where 1 yard equals 36 inches, or 3 feet.

Volume = (16/3) x (32/36) x (10/36) = 1.32 cubic yards.

Walls

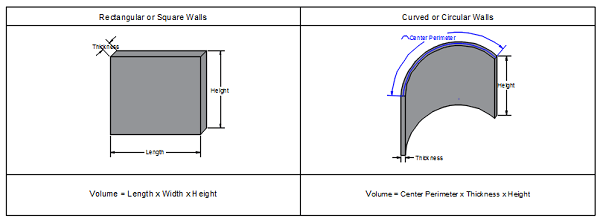
Walls are mostly rectangular, square, or curved in shape. However, even though curved or circular walls do exist, they can be theoretically converted to straight walls to simplify calculations (note: the volume of circular walls can be calculated in different ways, but this is the easiest). Hence, calculating yards of concrete for walls is somewhat similar to that of rectangular or square columns, with the length being significantly more.
For example, the cross-sectional area of rectangular and square walls equals (length x width). And the volume equals (length x width x height).
Whereas, for curved or circular walls, the method of theoretically converting these walls into straight walls is simple. Just measure the perimeter of the wall from its center, as shown in the above diagram, and consider it as straight length. Then, calculate the area and volume similar to rectangular and square walls.

Walls example

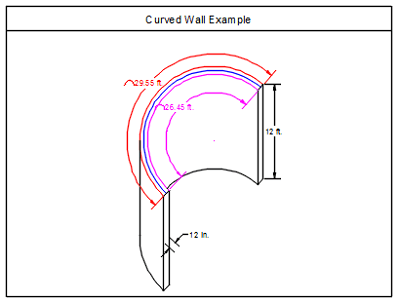
Considering the given example, the wall has an exterior perimeter of 29.55 feet, interior perimeter of 26.45 feet, height of 12 feet, and thickness of 12 inches. In order to theoretically convert this curved wall to a straight wall, determine the perimeter of the wall from its center.
Center perimeter = (exterior perimeter + interior perimeter)/2 = (29.55 + 26.5)/2 = 28 feet.
Hence, the following example theoretically represent a straight wall with a length of 28 feet, height of 12 feet, and thickness of 12 inches. In addition, calculating yards of concrete requires converting units from feet and inches to yards, where 1 yard equals 36 inches, or 3 feet.

Cross-sectional area = length x thickness = (28/3) x (12/36) = 3.11 square yards.
Volume = area x height = 3.11 square yards x (12/3) = 12.44 cubic yards.

Concrete Yards Calculator

You can also use tools that can help you calculate how many yards of concrete do you need for your project, just like The Ultimate Concrete Calculator (Cubic Meters, Cubic Yards, & Bags).

Questions

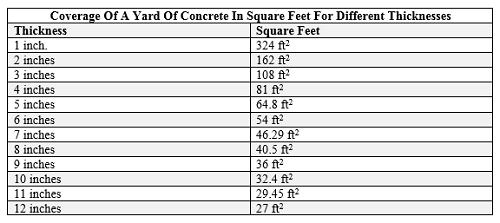
How many square feet in a yard of concrete?

Generally, a yard of concrete means a cubic yard, which resembles volume. Whereas, a square foot is an area unit. Hence, in order to calculate how many square feet in a yard of concrete, we should also consider thickness.

In a nutshell, the following table shows the concrete yard coverage in square feet for various thicknesses.

How many yards of concrete do I need for a 24x24x4 slab?

For a 24x24x4 slab, you will need exactly 7.11 cubic yards of concrete. Considering the slab of 24 feet x 24 feet x 4 inches, the required concrete yards or volume = area x thickness, as explained in this article. First, you have to convert feet into yards by dividing by 3, and inches to yards by dividing by 36.
Hence, required volume = 24/3 x 24/3 x 4/36 = 7.11 cubic yards of concrete.

How many yards of concrete do I need for a 30x30x4 slab?

For a slab of 30x30x4, you will need 11.11 cubic yards of concrete. Actually, the calculation is simple, in order to calculate the volume of the 30 feet x 30 feet x 4 inches slab, you need to convert the units from inches and feet to yards first. Hence, you will end up having the following equation, volume = area x thickness = 30/3 x 30/3 x 4/36 = 11.11 cubic yards.

How many yards of concrete do I need for a 10×10 slab?

To calculate the yardage for a 10×10 slab, you need do to know its thickness first. For a 10×10 slab:

• 4″ thickness requires 1.234 cubic yards.
• 5″ thickness requires 1.543 cubic yards.
• 6″ thickness requires 1.851 cubic yards of concrete.

How many yards of concrete do I need for a 40×60 slab with thickness of 5 inches?

For a 40×60 slab, 5 inches thick, you need 37.04 yards of concrete. You can calculate the yardage as previously explained, 40/3 x 60/3 x 5/36 = 37.04 cubic yards.

How many yards of concrete do I need for 800 square feet slab 6 inches deep?

For 800 square feet slab, 6 inches thick, you will need exactly 14.81 yards of concrete. The formula is as follows, 800/9 x 6/36 = 14.81 cubic yards. We divide by 9 in order to convert square feet into square yards, and by 36 to convert inches to yards.

How many cubic feet in a yard of concrete?

One yard of concrete equals 27 cubic feet. In fact, each linear yard makes 3 linear feet. Hence, to convert cubic yards to a cubic feet, multiply by 3 three times (3x3x3 = 27).

How to figure concrete yardage for footers?

Footers are generally rectangular or square shaped, so the calculating the yardage is as simple as multiplying the length by width by thickness, similar to what explained in the slabs or beams sections. For more complex footer shapes, such as sloped or stepped footing, you can divide the shape into regular shapes, and add or subtract volumes to figure the required concrete yardage for the original shape.

How many yards of concrete in a truck?

There are different types of trucks which can hold different quantities of concrete. However, the most common trucks often hold between 8 and 11 yards of concrete. Such trucks can usually hold more, however, depending on the location or state, they are often limited to 8, 9, 10, or 11 yards of concrete.